お土産の買い方（2）
2020.07.06
守屋 誠司
『玉川通信』2018年8月号の続きで、一点だけのお土産を買うときのコツと利用方法を書く。
海外に行った際にノミの市を覗いたり、国内のネットオークションで落札したりして、人形をよく買う。人形を選ぶ基準は、「算数科指導法」テキストp.133に掲載してあるような機能的曲面体の人形や平面で囲まれている多面体の人形である。
写真1は、ヘディングの瞬間を捉えたハンガリーのヘレンド社の磁器人形である。ユニホームのシワや筋肉の動きまで表現され、実にリアルである。写真2は、ドイツの錫人形で、中世の職人シリーズの2つである。面や立体の授業を行う際に、これらの人形を教材にする。はじめに、人形を見せながら運動をしている人形を作ることを知らせ、詳しく観察させて動機づけをする。次に、体の表面の曲がり具合や骨格の学習をする。曲線や曲面の曲がり具合を曲率という。胸はゆったり曲がった曲面で曲率は小さい、それに比べて脇あたりは、キュッと曲がっていて曲率が大きい曲面である。胴体は決して円柱ではない。曲率に関しては「算数」テキストp.174に詳しい。また、関節のところで体は曲がるため、適当な場所で心材を曲げてはいけないことも学習する。その後で、市販の心材を使って運動ポーズを作る。それに麻紐を巻き、紙粘土で厚みを付け、色を塗って完成させる。写真3は、小学校1年生が運動をする人を作成している過程である。曲率の考え方と骨格の学習をすれば1年生でもこんなにリアルな人形を作れる。
写真1 ヘレンド社製
写真2 錫製の職人人形（ドイツ）
写真3 人形の制作過程（1年生）スクーリングでは、写真4の刺繍画を作る。曲率概念を学修した後、曲線を円近似し長さを計測した上で、絵柄の周りに計測結果に基づいて切り取ってあった毛糸を貼り、立体的に仕上げる。
次に平面で囲まれている多面体のお土産を紹介する。写真5は奈良の一刀彫り、写真6は米沢市の笹野一刀彫りである。
写真4 刺繍画と事前の作図と計測
写真5 猩々
写真6 お鷹ぽっぽ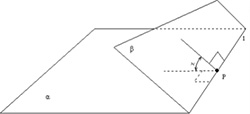
図1 二面角の定義多面体で重要な概念は図1の二面角である。小学校では、二面角の大きさが90度の立体である直方体や立方体、多角柱を扱う。しかし、一般的には90度以外も重要である。そこで、まずは、多角柱の応用である箱車作りから始める。写真7はスクーリングで学生が作ったディズニー・パレードである。ケント紙に展開図をかいて色を塗り、組み立てた。
写真7 角柱の応用。天井と側面の二面角が90度である次に二面角が一般角である立体作りを扱う。写真8は、博物館で購入した方解石の結晶である。6つの平行四辺形で囲まれている立体で、「平行六面体」といわれる。この立体をいきなり作るのは難しいため、最初にジャガイモから立体を切り出す。それをケント紙の上で転がしながら面の形を写し取る（写真9）。なお、多面体の最終課題は、写真7とは違い、写真10のような天井と側面の二面角が90度より大きくなっている車を作る。 教師に必要な立体学習の詳細はスクーリングで扱うため、是非とも参加して欲しい。
写真8 方解石の結晶
写真9 平行六面体の展開図
写真10 ワゴン車（学生の作品）プロフィール
- 教育学部教育学科 通信教育課程 教授
- 東北大学博士課程情報科学研究科修了。博士（情報科学）。
- 山梨県の公立小・中学校の教諭を勤めた後に、兵庫女子大学専任講師、山形大学助教授、京都教育大学教授を歴任。この間に山形県立保健医療大学、福島大学、大阪教育大学等の非常勤講師を務めた。京都教育大学名誉教授。山梨大学・東京福祉大学非常勤講師。
- 専門は数学教育学で、教材開発や教育方法、数学的認知、比較数学教育、数学の文化史を研究する。
- 数学教育学会理事。
- 著書：『小学校指導法 算数』（玉川大学）編著・他多数。
